Essence and properties of the production function. Production function: concept, properties

economic function rural costs

In order to describe the behavior of a company, it is necessary to know how much of a product it can produce using resources in certain volumes. We will proceed from the assumption that the company produces a homogeneous product, the quantity of which is measured in natural units - tons, pieces, meters, etc. The dependence of the amount of product that a firm can produce on the volume of resource inputs is called the production function.

But an enterprise can carry out the production process in different ways, using different technological methods, different options for organizing production, so the amount of product obtained with the same expenditure of resources may be different. Firm managers should reject production options that give lower output if a higher output can be obtained with the same costs of each type of resource. Likewise, they should reject options that require more input from at least one input without increasing yield or reducing the input of other inputs. Options rejected for these reasons are called technically ineffective.

Let's say your company produces refrigerators. To make the body, you need to cut sheet iron. Depending on how a standard sheet of iron is marked and cut, more or fewer parts can be cut out of it; Accordingly, to manufacture a certain number of refrigerators, less or more standard sheets of iron will be required. At the same time, the consumption of all other materials, labor, equipment, and electricity will remain unchanged. This production option, which could be improved by more rational cutting of iron, should be considered technically ineffective and rejected.

Technically efficient are production options that cannot be improved either by increasing the production of a product without increasing the consumption of resources, or by reducing the costs of any resource without reducing output and without increasing the costs of other resources. The production function takes into account only technically efficient options. Its value is the largest amount of product that an enterprise can produce given the volume of resource consumption.

Let us first consider the simplest case: an enterprise produces a single type of product and consumes a single type of resource. An example of such production is quite difficult to find in reality. Even if we consider an enterprise that provides services at clients’ homes without the use of any equipment and materials (massage, tutoring) and uses only the labor of workers, we would have to assume that workers walk around clients on foot (without using transport services) and negotiate with clients without the help of mail and telephone.

So, an enterprise, spending a resource in quantity x, can produce a product in quantity q. Production function

establishes a connection between these quantities. Note that here, as in other lectures, all volumetric quantities are flow-type quantities: the volume of resource input is measured by the number of units of the resource per unit of time, and the volume of output is measured by the number of units of product per unit of time.

In Fig. 1 shows the graph of the production function for the case under consideration. All points on the graph correspond to technically effective options, in particular points A and B. Point C corresponds to an ineffective option, and point D to an unattainable option.

Rice. 1.

A production function of type (1), which establishes the dependence of the volume of production on the volume of costs of a single resource, can be used not only for illustrative purposes. It is also useful when the consumption of only one resource can change, and the costs of all other resources for one reason or another should be considered as fixed. In these cases, the dependence of production volume on the costs of a single variable factor is of interest.

Much greater diversity appears when considering a production function that depends on the volumes of two resources consumed:

q = f(x 1 , x 2), (2)

Analysis of such functions makes it easy to move to the general case when the number of resources can be any. In addition, the production functions of two arguments are widely used in practice when a researcher is interested in the dependence of the volume of product output on the most important factors - labor costs (L) and capital (K):

q = f(L, K), (3)

The graph of a function of two variables cannot be depicted on a plane. A production function of type (2) can be represented in three-dimensional Cartesian space, two coordinates of which (x 1 and x 2) are plotted on the horizontal axes and correspond to resource costs, and the third (q) is plotted on the vertical axis and corresponds to product output (Fig. 2) . The graph of the production function is the surface of the “hill”, which increases with each of the coordinates x 1 and x 2. Construction in Fig. 1 can be considered as a vertical section of the “hill” by a plane parallel to the x 1 axis and corresponding to a fixed value of the second coordinate x 2 = x * 2.

Rice. 2.

economic rural costs

The horizontal section of the “hill” combines production options characterized by a fixed output of product q = q* with various combinations of inputs of the first and second resources. If the horizontal section of the “hill” surface is depicted separately on a plane with coordinates x 1 and x 2, a curve will be obtained that combines such combinations of resource inputs that make it possible to obtain a given fixed volume of product output (Fig. 3). Such a curve is called the isoquant of the production function (from the Greek isoz - the same and the Latin quantum - how much).

Rice. 3.

Let us assume that the production function describes output depending on labor and capital inputs. The same amount of output can be obtained with different combinations of inputs of these resources. You can use a small number of machines (i.e., get by with a small investment of capital), but you will have to spend a large amount of labor; It is possible, on the contrary, to mechanize certain operations, increase the number of machines and thereby reduce labor costs. If for all such combinations the largest possible output remains constant, then these combinations are represented by points lying on the same isoquant.

By fixing the volume of product output at a different level, we obtain another isoquant of the same production function. Having performed a series of horizontal sections at various heights, we obtain the so-called isoquant map (Fig. 4) - the most common graphical representation of the production function of two arguments. It is similar to a geographical map, on which the terrain is depicted with contour lines (otherwise known as isohypses) - lines connecting points lying at the same height.

It is easy to see that the production function is in many ways similar to the utility function in consumption theory, the isoquant to the indifference curve, and the isoquant map to the indifference map. Later we will see that the properties and characteristics of the production function have many analogies in the theory of consumption. And this is not a matter of simple similarity. In relation to resources, the firm behaves as a consumer, and the production function characterizes precisely this side of production - production as consumption. This or that set of resources is useful for production insofar as it allows obtaining the appropriate volume of output of the product. We can say that the values ​​of the production function express the utility for producing the corresponding set of resources. Unlike consumer utility, this “utility” has a completely definite quantitative measure - it is determined by the volume of products produced.

Rice. 4.

The fact that the values ​​of the production function refer to technically efficient options and characterize the highest output when consuming a given set of resources also has an analogy in consumption theory. The consumer can use the purchased goods in different ways. The utility of a purchased set of goods is determined by the way they are used in which the consumer receives the greatest satisfaction.

However, despite all the noted similarities between consumer utility and “utility” expressed by the values ​​of the production function, these are completely different concepts. The consumer himself, based only on his own preferences, determines how useful this or that product is for him - by buying or rejecting it. A set of production resources will ultimately be useful to the extent that the product that is produced using these resources is accepted by the consumer.

Since the production function has the most general properties of the utility function, we can further consider its main properties without repeating the detailed arguments given in Part II.

We will assume that an increase in the costs of one of the resources while maintaining constant costs of the other allows us to increase the output. This means that the production function is an increasing function of each of its arguments. Through each point of the resource plane with coordinates x 1, x 2 there passes a single isoquant. All isoquants have a negative slope. The isoquant corresponding to a higher product yield is located to the right and above the isoquant for a lower yield. Finally, we will consider all isoquants to be convex in the direction of the origin.

In Fig. Figure 5 shows some isoquant maps that characterize various situations that arise during the production consumption of two resources. Rice. 5a corresponds to absolute mutual substitution of resources. In the case presented in Fig. 5b, the first resource can be completely replaced by the second: the isoquant points located on the x2 axis show the amount of the second resource that allows one to obtain a particular product output without using the first resource. Using the first resource allows you to reduce the costs of the second, but it is impossible to completely replace the second resource with the first. Rice. 5,c depicts a situation in which both resources are necessary and neither of them can be completely replaced by the other. Finally, the case presented in Fig. 5d, is characterized by absolute complementarity of resources.

Rice. 5.

The production function, which depends on two arguments, has a fairly clear representation and is relatively simple to calculate. It should be noted that economics uses the production functions of various objects - enterprises, industries, national and world economies. Most often these are functions of the form (3); sometimes a third argument is added - the cost of natural resources (N):

q = f(L, K, N), (4)

This makes sense if the amount of natural resources involved in production activities is variable.

Applied economic research and economic theory use different types of production functions. In applied calculations, the requirements of practical computability force us to limit ourselves to a small number of factors, and these factors are considered enlarged - “labor” without division into professions and qualifications, “capital” without taking into account its specific composition, etc. In the theoretical analysis of production, one can escape from the difficulties of practical computability.

Raw materials of different grades should be considered as different types of resources, just like machines of different brands or labor that differs in professional and qualification characteristics. Thus, the production function used in theory is a function of a large number of arguments:

q = f(x 1 , x 2 ,..., x n), (5)

The same approach was used in the theory of consumption, where the number of types of goods consumed was not limited in any way.

Everything that was previously said about the production function of two arguments can be transferred to a function of the form (4), of course, with reservations regarding dimensionality. Isoquants of function (4) are not plane curves, but n-dimensional surfaces. Nevertheless, we will continue to use “flat isoquants” - both for illustrative purposes and as a convenient means of analysis in cases where the costs of two resources are variable, and the rest are considered fixed.

The types of production functions are presented in Table 1.

Table 1. Types of production functions

PF name	Two-factor PF	Usage
1. Function with fixed proportions of factors (Leontief PF)		Designed for modeling strictly deterministic technologies that do not allow deviations from technological standards for the use of resources per unit of production.
2. Cobb-Douglas PF		Used to describe medium-scale objects (from an industrial association to an industry), characterized by sustainable, stable functioning.
3. Linear PF		It is used to model large-scale systems (large industry, industry as a whole), in which product output is the result of the simultaneous functioning of many different technologies.
4. PF Allen		Intended to describe production processes in which excessive growth of any of the factors has a negative impact on output. Typically used to describe small-scale PSs with limited resource processing capabilities.
5. PF of constant elasticity of factor substitution (PEZ or CES)		It is used in cases where there is no accurate information about the level of interchangeability of production factors and there is reason to assume that this level does not change significantly when the volume of resources involved changes.
6. PF with linear elasticity of factor substitution (LES)
7. Solow function		It can be used in approximately the same situations as the PF PEZ, but the premises underlying it are weaker than those of the PEZ. Recommended when the assumption of homogeneity seems unjustified. Can simulate systems of any scale.

Neoclassical models of economic growth are built on the basis of the production function and are based on the assumptions of full employment, price flexibility in all markets, and complete interchangeability of production factors. Attempts to explore the extent to which the quality of factors of production (their productivity) and various proportions in their combination affect economic growth led to the creation of the Cobb-Douglas production function model.

The Cobb-Douglas function was first proposed by Knut Wicksell. In 1928, tested on statistical data by Charles Cobb and Paul Douglas in the work “A Theory of Production” (mar., 1928). This article attempted to empirically determine the impact of capital and labor expended on volume of output in the US manufacturing industry.

The Cobb-Douglas production function is the dependence of the volume of production Q on the labor L and capital K creating it.

General view of the function:

where A is the technological coefficient,

b - labor elasticity coefficient, a

c -- capital elasticity coefficient.

For the first time, the Cobb-Douglas Function was obtained as a result of a mathematical transformation of the simplest two-factor production function y = f(x1, x2), reflecting the relationship between the volume of output y and two types of resources: material x1 (costs of raw materials, energy, transport and other resources) and labor x2. The Cobb-Douglas function shows what share of the total product is rewarded to the production factor involved in its creation.

Thus, an unambiguous quantitative determination of the share of each production resource in the final product is difficult, since production is possible only with the interaction of all factors and the influence of each factor depends both on the volume of its use and on the volume of use of other resources.

The construction of production functions allows, although not absolutely accurately, to determine the influence of each resource on the production result, to make a forecast regarding changes in production volume with changes in the volume of resources, to determine the optimal combination of resources to obtain a given amount of output.

The production function characterizes the maximum possible output that can be obtained using a given combination of resources.

In production theory, a two-factor production function of the form Q = f(L, K) is traditionally used, characterizing the relationship between the volume of output (Q) and the quantities of labor (L) and capital (K) resources used. This is explained not only by the convenience of graphical display, but also by the fact that the specific consumption of materials in many cases depends little on the volume of output, and such a factor as production area is usually considered together with capital.

The production function is constructed for this technology. Improvements in technology that increase the maximum achievable volume of output for any combination of factors are reflected by a new production function.

Although production functions are different for different types of production, they nevertheless have common properties.

There is a limit to the increase in production volume that can be achieved by increasing the costs of one resource, all other things being equal.

This assumes, for example, that in an enterprise, given the number of machines and production facilities, there is a limit to increasing production by attracting more workers.

The increase in production that can be achieved by increasing the number of workers employed in it will obviously approach zero. Indeed, it is possible to reach a point where each new worker in the enterprise will contribute to a reduction rather than an increase in output. This can happen if a worker is not provided with the equipment to do the job and his presence interferes with the work of other workers and reduces their efficiency.

There is a certain mutual complementarity of production factors; in addition, without a reduction in production volume, a certain interchangeability of these factors is possible.

Workers do their jobs more efficiently if they are equipped with all the necessary tools. Likewise, tools may be useless if workers are not qualified to use them.

4.1.1.ISOQUANT

Isoquant (line of equal output) is a curve representing an infinite number of combinations of production factors (resources) that provide the same output.

Isoquants for the production process mean the same as indifference curves for the consumption process and have similar properties: they have a negative slope, are convex relative to the origin, and do not intersect each other. The further the isoquant is located from the origin, the greater the volume of output it represents. Moreover, in contrast to indifference curves, where the total consumer satisfaction cannot be accurately measured, isoquants show real production levels: 100 units, 300 thousand units. and so on.

Isoquants (like indifference curves) can have different configurations (Fig. 4.1).

Rice. 4.1. Possible isoquant configurations

Linear isoquant (Fig. 4.1, a) assumes perfect substitutability of production resources, so that a given output can be obtained using either labor, or capital alone, or using infinitely possible combinations of both resources. The isoquant shown in Fig. 4.1, b, is typical for the case of strict complementarity of resources: only one method of producing a given product is known, labor and capital are combined in the only possible ratio.

In Fig. 4.1, c shows a broken isoquant, suggesting a limited possibility of substituting resources (only at break points) and the presence of only a few production methods. Finally, in Fig. 4.1, d presents an isoquant, which assumes the possibility of continuous substitutability of resources within certain boundaries, beyond which the replacement of one factor by another is technically impossible.

Many engineers, entrepreneurs, and production workers consider the broken isoquant to most realistically represent the production capabilities of most modern industries. However, traditional economic theory usually operates with smooth isoquants like the one shown in Fig. 4.1, d, since their analysis does not require the use of complex mathematical methods. In addition, isoquants of this type can be considered as a kind of approximate approximation of a broken isoquant. By increasing the number of production methods and thus increasing the number of break points, we can (in the limit) represent a broken isoquant as a smooth curve.

4.1.2. INTERCHANGEABILITY OF PRODUCTION FACTORS

The slope of the isoquants characterizes the marginal rate of technical substitution of one factor by another:

. (4.1)

The marginal rate of technical substitution of capital by labor is the amount by which capital can be reduced by using one additional unit of labor for a fixed volume of output (Q = const).

Question 11: In the short run, a competitive firm that maximizes profits or minimizes losses will not continue production if:

a) the price of the product is below the minimum average cost;

b) average fixed costs are higher than the price of the product;

c) the price of the product is below the minimum average variable cost;

d) the price of the product is below marginal cost;

d) total revenue does not cover the firm's total costs.

The correct answer is d).

The firm will produce the optimal amount of output if price equals marginal cost. If the firm continues to produce, the price will exceed marginal cost and the firm will begin to incur additional losses. Therefore, either the firm's overall profits will begin to decline, or its losses will begin to increase. If the product price is below minimum average cost (a) or average fixed cost is above price (b) or total revenue does not cover total costs (e), the firm will be unprofitable. If the price of a product is below average variable cost (c), then the firm should exit the market.

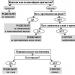
Each company, having undertaken the production of a specific product, strives to achieve maximum profit. Problems associated with product production can be divided into three levels:

1. An entrepreneur may be faced with the question of how to produce a given quantity of products at a certain enterprise. These problems relate to issues of short-term minimization of production costs;
2. the entrepreneur can solve questions about the production of the optimal, i.e. bringing greater profit, the amount of production at a particular enterprise. These questions concern long-term profit maximization;
3. An entrepreneur may be faced with the task of determining the most optimal size of an enterprise. Similar questions relate to long-term profit maximization.

The optimal solution can be found based on an analysis of the relationship between costs and production volume (output). After all, profit is determined by the difference between revenue from sales of products and all costs. Both revenue and costs depend on production volume. Economic theory uses the production function as a tool for analyzing this relationship.

The production function determines the maximum volume of output for each given amount of input. This function describes the relationship between resource costs and output, allowing you to determine the maximum possible volume of output for each given amount of resources, or the minimum possible amount of resources to ensure a given volume of output. The production function summarizes only technologically efficient methods of combining resources to ensure maximum output. Any improvement in production technology that contributes to an increase in labor productivity determines a new production function.

PRODUCTION FUNCTION - a function that reflects the relationship between the maximum volume of a product produced and the physical volume of factors of production at a given level of technical knowledge.

Since the volume of production depends on the volume of resources used, the relationship between them can be expressed as the following functional notation:

Q = f(L,K,M),

where Q is the maximum volume of products produced using a given technology and certain factors of production;
L – labor; K – capital; M – materials; f – function.

The production function for a given technology has properties that determine the relationship between the volume of production and the number of factors used. For different types of production, production functions are different, however? they all have common properties. Two main properties can be distinguished.

1. There is a limit to the growth of output that can be achieved by increasing the costs of one resource, all other things being equal. Thus, in a firm with a fixed number of machines and production facilities, there is a limit to the growth of output by increasing additional workers, since the worker will not be provided with machines for work.
2. There is a certain mutual complementarity (completeness) of production factors, however, without a decrease in output, a certain interchangeability of these production factors is also likely. Thus, various combinations of resources can be used to produce a good; it is possible to produce this good using less capital and more labor, and vice versa. In the first case, production is considered technically efficient in comparison with the second case. However, there is a limit to how much labor can be replaced by more capital without reducing production. On the other hand, there is a limit to the use of manual labor without the use of machines.

In graphical form, each type of production can be represented by a point, the coordinates of which characterize the minimum resources required to produce a given volume of output, and the production function - by an isoquant line.

Having considered the production function of the company, we move on to characterize the following three important concepts: total (total), average and marginal product.

Rice. a) Total product (TP) curve; b) curve of average product (AP) and marginal product (MP)

In Fig. shows the total product (TP) curve, which varies depending on the value of the variable factor X. Three points are marked on the TP curve: B – inflection point, C – point that belongs to the tangent coinciding with the line connecting this point to the origin, D – point of maximum TP value. Point A moves along the TP curve. By connecting point A to the origin of coordinates, we obtain line OA. Dropping the perpendicular from point A to the x-axis, we obtain a triangle OAM, where tg a is the ratio of the side AM to OM, i.e., the expression of the average product (AP).

Drawing a tangent through point A, we obtain an angle P, the tangent of which will express the limiting product MP. Comparing the triangles LAM and OAM, we find that up to a certain point the tangent P is greater than tan a. Thus, marginal product (MP) is greater than average product (AP). In the case when point A coincides with point B, the tangent P takes on its maximum value and, therefore, the marginal product (MP) reaches its greatest volume. If point A coincides with point C, then the values ​​of the average and marginal products are equal. The marginal product (MP), having reached its maximum value at point B (Fig. 22, b), begins to contract and at point C it intersects with the graph of the average product (AP), which at this point reaches its maximum value. Then both the marginal and average product decrease, but the marginal product decreases at a faster pace. At the point of maximum total product (TP), the marginal product MP = 0.

We see that the most effective change in the variable factor X is observed on the segment from point B to point C. Here the marginal product (MP), having reached its maximum value, begins to decrease, the average product (AP) still increases, the total product (TP) receives the greatest growth.

Thus, the production function is a function that allows us to determine the maximum possible volume of output for various combinations and quantities of resources.

In production theory, a two-factor production function is traditionally used, in which the volume of production is a function of the use of labor and capital resources:

Q = f (L, K).

It can be presented in the form of a graph or curve. In the theory of producer behavior, under certain assumptions, there is a single combination of resources that minimizes resource costs for a given volume of production.

Calculation of a firm's production function is a search for the optimum, among many options involving various combinations of production factors, one that gives the maximum possible volume of output. In an environment of rising prices and cash costs, the firm, i.e. costs of purchasing factors of production, the calculation of the production function is focused on searching for an option that would maximize profits at the lowest costs.

The calculation of the firm's production function, seeking to achieve a balance between marginal costs and marginal revenue, will focus on finding an option that will provide the required output at minimal production costs. Minimum costs are determined at the stage of calculations of the production function by the method of substitution, displacing expensive or increased in price factors of production with alternative, cheaper ones. Substitution is carried out using a comparative economic analysis of interchangeable and complementary factors of production at their market prices. A satisfactory option will be one in which the combination of production factors and a given volume of output meets the criterion of lowest production costs.

There are several types of production function. The main ones are:

1. Nonlinear PF;
2. Linear PF;
3. Multiplicative PF;
4. PF "input-output".

Production function and choice of optimal production size

A production function is the relationship between a set of factors of production and the maximum possible output produced by that set of factors.

The production function is always specific, i.e. intended for this technology. New technology - new productivity function.

Using the production function, the minimum amount of input required to produce a given volume of product is determined.

Production functions, regardless of what type of production they express, have the following general properties:

1. Increasing production volume due to increasing costs for only one resource has a limit (you cannot hire many workers in one room - not everyone will have space).
2. Factors of production can be complementary (workers and tools) and interchangeable (production automation).

In its most general form, the production function looks like this:

Q = f(K,L,M,T,N),

where L is the volume of output;
K – capital (equipment);
M – raw materials, materials;
T – technology;
N – entrepreneurial abilities.

The simplest is the two-factor Cobb-Douglas production function model, which reveals the relationship between labor (L) and capital (K). These factors are interchangeable and complementary

Q = AK α * L β,

where A is the production coefficient, showing the proportionality of all functions and changes when the basic technology changes (after 30-40 years);
K, L – capital and labor;
α, β – coefficients of elasticity of production volume in terms of capital and labor costs.

If = 0.25, then an increase in capital costs by 1% increases production volume by 0.25%.

Based on the analysis of elasticity coefficients in the Cobb-Douglas production function, we can distinguish:

1. proportionally increasing production function when α + β = 1 (Q = K 0.5 * L 0.2).
2. disproportionately – increasing α + β > 1 (Q = K 0.9 * L 0.8);
3. decreasing α + β< 1 (Q = K 0,4 * L 0,2).

The optimal size of enterprises is not absolute in nature, and therefore cannot be established outside of time and outside the area of ​​location, since they are different for different periods and economic regions.

The optimal size of the designed enterprise should ensure a minimum of costs or a maximum of profits, calculated using the formulas:

Тс+С+Тп+К*En_ – minimum, П – maximum,

where Тс – costs of delivery of raw materials;
C – production costs, i.e. production cost;
Тп – costs of delivering finished products to consumers;
K – capital costs;
En – standard efficiency coefficient;
P – enterprise profit.

Sl., the optimal size of enterprises is understood as those that provide the target of the plan for production output and the increase in production capacity with a minus of reduced costs (taking into account capital investments in related industries) and the highest possible economic efficiency.

The problem of optimizing production and, accordingly, answering the question of what the optimal size of an enterprise should be, faced Western entrepreneurs, presidents of companies and firms with all its severity.

Those that failed to achieve the required scale found themselves in the unenviable position of high-cost producers, condemned to an existence on the brink of ruin and eventual bankruptcy.

Today, however, those American companies that still strive to succeed in the competitive struggle through economies of concentration of production are not winning as much as they are losing. In modern conditions, this approach initially leads to a decrease in not only flexibility, but also production efficiency.

In addition, entrepreneurs remember: small enterprise size means less investment and, therefore, less financial risk. As for the purely managerial side of the problem, American researchers note that enterprises with more than 500 employees become poorly managed, slow and poorly responsive to emerging problems.

Therefore, a number of American companies in the 60s decided to disaggregate their branches and enterprises in order to significantly reduce the size of the primary production units.

In addition to the simple mechanical disaggregation of enterprises, production organizers carry out radical reorganization within enterprises, forming command and brigade organizations in them. structures instead of linear-functional ones.

When determining the optimal enterprise size, firms use the concept of minimum efficient size. It is simply the smallest level of production at which the firm can minimize its long-run average cost.

Production function and selection of optimal production size.

Production is any human activity involving the transformation of limited resources - material, labor, natural - into finished products. The production function characterizes the relationship between the amount of resources used (factors of production) and the maximum possible volume of output that can be achieved provided that all available resources are used in the most rational way.

The production function has the following properties:

1. There is a limit to the increase in production that can be achieved by increasing one resource and holding other resources constant. If, for example, in agriculture we increase the amount of labor with constant amounts of capital and land, then sooner or later a moment comes when output stops growing.
2. Resources complement each other, but within certain limits their interchangeability is possible without reducing output. Manual labor, for example, can be replaced by the use of more machines, and vice versa.
3. The longer the time period, the more resources can be revised. In this regard, instantaneous, short and long periods are distinguished. An instantaneous period is a period when all resources are fixed. Short period - a period when at least one resource is fixed. A long period is a period when all resources are variable.

Usually in microeconomics a two-factor production function is analyzed, reflecting the dependence of output (q) on the amount of labor used ( L) and capital ( K). Let us recall that capital refers to the means of production, i.e. the number of machines and equipment used in production and measured in machine hours. In turn, the amount of labor is measured in man-hours.

Typically, the production function in question looks like this:

q = AK α L β

A, α, β - specified parameters. Parameter A is the coefficient of total productivity of production factors. It reflects the impact of technical progress on production: if a manufacturer introduces advanced technologies, the value of A increases, i.e., output increases with the same amounts of labor and capital. Parameters α and β are the elasticity coefficients of output for capital and labor, respectively. In other words, they show by how many percent output changes when capital (labor) changes by one percent. These coefficients are positive, but less than one. The latter means that when labor with constant capital (or capital with constant labor) increases by one percent, production increases to a lesser extent.

Construction of an isoquant

The given production function suggests that the producer can replace labor with capital and capital with labor, leaving output unchanged. For example, in agriculture in developed countries, labor is highly mechanized, i.e. There are many machines (capital) per worker. On the contrary, in developing countries the same output is achieved through a large amount of labor with little capital. This allows you to construct an isoquant (Fig. 8.1).

An isoquant (line of equal product) reflects all combinations of two factors of production (labor and capital) at which output remains unchanged. In Fig. 8.1 next to the isoquant the corresponding release is indicated. Yes, release q 1, achievable by using L 1 labor and K 1 capital or using L 2 labor and K 2 capital.

Rice. 8.1. Isoquant

Other combinations of labor and capital volumes are possible, the minimum required to achieve a given output.

All combinations of resources corresponding to a given isoquant reflect technically efficient methods of production. Production method A is technically efficient in comparison with method B if it requires the use of at least one resource in smaller quantities, and all others in smaller quantities, in comparison with method B. Accordingly, method B is technically ineffective in comparison with A. Technically ineffective production methods are not used by rational entrepreneurs and are not part of the production function.

From the above it follows that an isoquant cannot have a positive slope, as shown in Fig. 8.2.

The dotted line reflects all technically inefficient production methods. In particular, in comparison with method A, method B to ensure equal output ( q 1) requires the same amount of capital but more labor. It is obvious, therefore, that method B is not rational and cannot be taken into account.

Based on the isoquant, the marginal rate of technical substitution can be determined.

The marginal rate of technical replacement of factor Y by factor X (MRTS XY) is the amount of factor Y(for example, capital), which can be abandoned when the factor increases X(for example, labor) by 1 unit so that output does not change (we remain at the same isoquant).

Rice. 8.2. Technically efficient and inefficient production

Consequently, the marginal rate of technical replacement of capital by labor is calculated by the formula
For infinitesimal changes in L and K, it is
Thus, the marginal rate of technical substitution is the derivative of the isoquant function at a given point. Geometrically, it represents the slope of the isoquant (Fig. 8.3).

Rice. 8.3. Limit rate of technical replacement

When moving from top to bottom along an isoquant, the marginal rate of technical replacement decreases all the time, as evidenced by the decreasing slope of the isoquant.

If the producer increases both labor and capital, then this allows him to achieve greater output, i.e. move to a higher isoquant (q2). An isoquant located to the right and above the previous one corresponds to a larger volume of output. The set of isoquants forms an isoquant map (Fig. 8.4).

Rice. 8.4. Isoquant map

Special cases of isoquants

Let us recall that the given isoquants correspond to the production function of the form q = AK α L β. But there are other production functions. Let us consider the case when there is perfect substitutability of factors of production. Let us assume, for example, that skilled and unskilled loaders can be used in warehouse work, and the productivity of a qualified loader is N times higher than that of an unskilled loader. This means that we can replace any number of qualified movers with unqualified movers at a ratio of N to one. Conversely, you can replace N unqualified loaders with one qualified one.

The production function then has the form: q = ax + by, Where x- number of qualified workers, y- number of unskilled workers, A And b- constant parameters reflecting the productivity of one skilled and one unskilled worker, respectively. The ratio of coefficients a and b is the maximum rate of technical replacement of unskilled loaders with qualified ones. It is constant and equal to N: MRTSxy = a/b = N.

Let, for example, a qualified loader be able to process 3 tons of cargo per unit time (this will be coefficient a in the production function), and an unskilled loader - only 1 ton (coefficient b). This means that the employer can refuse three unqualified loaders, additionally hiring one qualified loader, so that the output (total weight of the processed cargo) remains the same.

The isoquant in this case is linear (Fig. 8.5).

Rice. 8.5. Isoquant with perfect substitutability of factors

The tangent of the isoquant slope is equal to the maximum rate of technical replacement of unskilled loaders with qualified ones.

Another production function is the Leontief function. It assumes strict complementarity of production factors. This means that factors can only be used in a strictly defined proportion, violation of which is technologically impossible. For example, an airline flight can be carried out normally with at least one aircraft and five crew members. At the same time, it is impossible to increase aircraft hours (capital) while simultaneously reducing man-hours (labor), and vice versa, and keep output constant. Isoquants in this case have the form of right angles, i.e. the maximum rates of technical replacement are equal to zero (Fig. 8.6). At the same time, it is possible to increase output (the number of flights) by increasing both labor and capital in the same proportion. Graphically, this means moving to a higher isoquant.

Rice. 8.6. Isoquants in the case of strict complementarity of production factors

Analytically, such a production function has the form: q = min (aK; bL), where a and b are constant coefficients reflecting the productivity of capital and labor, respectively. The ratio of these coefficients determines the proportion of use of capital and labor.

In our flight example, the production function looks like this: q = min(1K; 0.2L). The fact is that capital productivity here is one flight per plane, and labor productivity is one flight per five people or 0.2 flights per person. If an airline has an aircraft fleet of 10 aircraft and has 40 flight personnel, then its maximum output will be: q = min( 1 x 8; 0.2 x 40) = 8 flights. At the same time, two aircraft will be idle on the ground due to a lack of personnel.

Let us finally look at the production function, which assumes that there are a limited number of production technologies to produce a given quantity of output. Each of them corresponds to a certain state of labor and capital. As a result, we have a number of reference points in the “labor-capital” space, connecting which we obtain a broken isoquant (Fig. 8.7).

Rice. 8.7. Broken isoquants with a limited number of production methods

The figure shows that output in volume q1 can be obtained with four combinations of labor and capital, corresponding to points A, B, C and D. Intermediate combinations are also possible, achievable in cases where two technologies are used together to obtain a certain total output . As always, by increasing the quantities of labor and capital, we move to a higher isoquant.

It was previously shown that the representation of a production system in the form of a “black box” involves establishing a connection between production factors and the product using a functional relationship called production function (PF) . There is a strict mathematical definition of PF: PF is the equation of the hypersurface of effective technological processes, namely, it is a continuous differentiable function v=f(u) , describing the set effective technological processes. In other words, this function uniquely determines greatest set of products v , which can be produced for a specific set of factors u .

Aggregation of sets of factors and products of production allows us to reduce the hypersurface equation to the form:

That is, the connection (effective transformation) between aggregated factors of production and a single product.

Note that aggregation is understood as the operation of consolidation (summing) of the volumes of factors and products, if they are homogeneous goods, or the cost comparison of dissimilar goods ( indexes in statistics!). Also, PFs can be defined for systems of various scales - from production sites to the global economy. Issues of obtaining various types of mathematical dependencies in the PF are based on econometrics and regression analysis. In fact, we are talking about constructing simple or multiple regression equations.

Thus, a common production function in the analysis of production processes is the production function that relates the volume of output of a single product ( Y ) with aggregate labor factors ( L ) and capital ( TO ) for a certain period of time: Y = f(L,K) .

Note that from the point of view of management accounting, labor costs represent variable costs, and capital costs represent fixed production costs. Therefore, in the short run, the production system can only change labor inputs, but cannot change capital inputs. Consequently, changes in both factors are possible only in the long term.

Let's consider the general properties of the PF:

1. at x i =0 for any

This property means (similar to the first property of technological sets) that in the absence of the costs of one of the factors of production, a zero product is produced, that is, there are no factors - absolute substitutes. That is, only partial replacement of one factor by another is possible, and not complete. For a two-factor PF, accordingly, this property will mean: f(L,0)=0 And f(0,K)=0 .

2. for everyone

In fact, this property means that the productivity of any system is limited from above, that is, as the costs of factors increase, the amount of product produced will increase, and after reaching a certain critical value it will fall. Critical values ​​​​specify the boundary of the economic region, exit from which leads to a decrease in system productivity with further growth of production factors. Consequently, on the border of the economic area there are points at which .(??), and the quantity of the product produced will increase within the economic area with an increase in factors of production.

3. for everyone

This property means the concavity of the PF, and from an economic point of view it expresses the law decreasing marginal efficiency of production product with increasing factor costs (see. law of diminishing marginal utility in the consumer model).

4. - this property characterizes the linear homogeneity of the PF, that is, with a simultaneous change in the amount of factor inputs by l times, the amount of product produced will also change by l times.

The property of linear homogeneity also allows us to transform the PF into a function of one variable. For example, a two-factor PF can be reduced to a single-factor one:

Or: or where y – average labor productivity, To – capital-labor ratio.

PFs that have all the above properties are called neoclassical .

Let us consider in more detail the properties of neoclassical PFs.

Previously, the position was formulated that the PF is built on a variety of effective technological processes. Mathematically, the efficiency of the production process is determined by the value of the average and marginal products produced at certain costs of production factors.

Average product- factor of production - this is the ratio of the amount of product produced to the amount of factor expended x i for a period of time: . For a two-factor PF, we can obtain the ratios: and , which corresponds to the average capital productivity (the average amount of product produced per unit of capital) and average labor productivity (the average amount of product produced per unit of labor). ( An analogy can be drawn with consumer modeling). The concept of average product confirms the concavity of the PF: the higher the cost of a factor, the lower the average product.

Marginal product factor a x i is an additional product produced by the system at the cost of an additional unit of factor x i . Again, an analogy can be drawn between the concepts marginal product And marginal utility, the qualitative homogeneity of these concepts leads to the concept of the first partial derivative of the product y by cost factor x i as a quantitative measure of this limiting value:

And for a two-factor PF: and , which corresponds to the marginal capital productivity and marginal labor productivity ( marginal product of capital, marginal product of labor). Again, the marginal products of factors are always less than the average products, which is a consequence of the concavity of the PF.

The ratio of the marginal product to the average product gives the coefficient of elasticity of the product with respect to i -th factor of production ( similar to the elasticity coefficient of the demand function with respect to income):

For a two-factor PF we have:

Product elasticity coefficient according to i- mu factor shows by what percentage the quantity of product produced will change when costs increase i -th factor by one percent. Using elasticity coefficients, we can express the marginal product through the average:

The introduction of elasticity coefficients makes it possible to calculate the change in product output while simultaneously changing the volume of input factors:

The last property of the PF about homogeneity also leads to the concept of the degree of homogeneity of the PF, namely:

Where δ is the degree of homogeneity of the PF. The neoclassical PF is a homogeneous PF with a degree of homogeneity equal to one. Such functions are also called linearly homogeneous.

In general, for any homogeneous differentiable function with degree of homogeneity δ, Euler’s theorem is valid:

. This theorem has important economic implications, namely, the product produced can be represented as the sum of the contributions of each factor to the product produced.

For a two-factor PF that is linearly homogeneous (δ=1), Euler’s theorem leads to:

.

If the two-factor PF were not linearly homogeneous, then the following relation would be true:

, it follows that:

And to conclude our discussion of the properties of PF, let us consider how changes in the scale of production affect its efficiency.

For this purpose, the concepts of average and marginal product of the scale of production are introduced.

Average scale product– this is the ratio of the product obtained by increasing factors by l times to the scaling factor l:

Marginal product of scale of production is approximately equal to the partial derivative of the product obtained by increasing the factors by l times by the scaling factor:

Since the elasticity coefficient is the ratio of the marginal product to the average product, then elasticity of scale will be equal to:

That is, the coefficient of elasticity of production scale will always be equal to the degree of homogeneity of the PF.

And one more important property E l : for any homogeneous PF, the sum of the elasticity coefficients of the product by factors is equal to the elasticity coefficient of the production scale:

Analysis of the elasticity coefficient of production scale reveals that if E l >1, then the consolidation of production has a positive effect, since such production systems have higher efficiency when the scale of production increases. If E l <1, то увеличение масштаба производства приведет к снижению его эффективности, но уменьшение масштаба в этом случае даст повышение производительности системы. Для линейно-однородных ПФ изменение масштабов производства приводит всегда к пропорциональному изменению продукта, то есть производство инвариантно к изменению масштаба.

PF isoquants and isoclines

If we turn again to the method of analogy, then, as in the case of the consumer behavior model, in the theory of modeling production processes we can highlight the concept of a manufacturer's indifference curve. This concept can correspond to many sets of production factors, which correspond to the same amount of product produced, that is:

The set of points satisfying equality (4.1) is called isoquant PF ( iso- constant, quantity- quantity). Each isoquant corresponds to a different level of product production ( y ), and isoquants more distant from the zero point (inaction points) correspond to higher values y . Isoquants also have the same properties as indifference curves (they are parallel to each other, do not intersect with the abscissa and ordinate axes, etc.) For a two-factor PF, an isoquant will essentially express the functional dependence of capital costs on labor costs at a given level of product produced:

The manufacturer, varying technologies, can choose different combinations of production factors and maintain a constant level of production. According to the isoquant, an increase in one factor will lead to a decrease in another. Therefore, there must be a characteristic that allows one to evaluate the compensation of one factor by another. This characteristic is marginal rate of substitution(similar to the same characteristic in consumer utility theory):

, (4.2)

which shows how much of an increase in factor j will compensate for the reduction in factor i per unit so that the level of production of the product remains the same (factor substitution i factor j ).

Accordingly, the reverse replacement (of factor j by factor i) will be characterized by the reciprocal value: .

According to the relationship between the elasticity coefficient and the marginal product (4.1), the marginal rate of substitution can be expressed as:

(4.3)

According to (4.1) for a two-factor PF we have:

- the maximum rate of replacement of capital with labor;

- the maximum rate of replacement of labor with capital.

According to (4.3), for a two-factor model, the marginal rate of substitution can also be expressed through elasticity coefficients:

, Where To – capital-labor ratio.

Along with isoquants, an important role in the PF is played by isoclines – sets of points in the economic area for which the marginal rate of substitution i -th factor j -m is constant:

Using the concept of isocline (isocline), you can transform an arbitrary set of factors (L,K) included in the set (Y,MRS) , that is, solving the system of equations:

will be:

Homogeneous PF with a constant marginal rate of labor substitution with capital and degree of homogeneity δ=1 belongs to the class of linear functions, that is .

Thus, for a two-factor PF, each point of the isoquant is characterized by the costs of capital and labor or the marginal rate of substitution of labor with capital MRS LK and capital-labor ratio k . If we turn to the geometric representation, then MRS LK is equal to the angular coefficient of the tangent to a given isoquant point, and the value of k is the angular coefficient of the ray emerging from the origin and passing through a given isoquant point (see. Rice. 4.2).

Figure 4.2

For example, at the point IN the value of labor costs is greater than at the point A , therefore, the value MRS LK at the point IN less than at point A . Accordingly, point IN will correspond to a lower capital-labor ratio than at point A .

Thus, the connection between the change in the capital-labor ratio and the marginal rate of labor substitution for capital becomes obvious, that is, we again come to the concept of elasticity, namely the elasticity of the substitution of labor with capital, which shows how much percent the capital-labor ratio will change when the marginal rate of substitution of labor for capital changes by one percent :

(4.4)

It can also be shown graphically that as the curvature of the isoquant increases, the elasticity Eσ decreases (see Rice. 4.3).

Fig 4.3

Note that in both cases at points A And IN values MRS LK remain the same, and the value of the capital-labor ratio at the point A higher than at point IN . This implies another important property: for a homogeneous PF, the elasticity of labor substitution with capital depends only on the capital-labor ratio and remains constant along the rays emanating from the zero point.

Let us express the connection between MRS LK And k with constant elasticity Eσ . According to (4.4) we have:

(4.5)

Assuming dependency MRS LK(k) , we can write (4.5) in the form of an ordinary differential equation:

(4.6)

Integration (4.6) gives:

or after conversion:

, Where

Consequently, the condition of constancy of the elasticity of substitution of labor with capital gives a power-law relationship between the quantities MRS LK And k . Accordingly, the case of unit elasticity will correspond to a linear relationship between the indicated quantities:

The introduction of the concept of constant elasticity of substitution led to the general form of a homogeneous PF, for which the elasticity of factor substitution is constant. Such PFs are called PFs CES class (Constant Elasticity of Substitution). Functions of this class were first proposed Arrow by Kenneth And Solow by Robert in 1961. The functions of this class assume that the replacement of labor with capital is possible only within certain limits and there are no technologies that would allow the production of a given amount of product at costs of production factors below certain critical values. (Geometrically, this means that it is possible to construct asymptotes to the isoquant, and they will correspond to the minimum possible values ​​of labor and capital. It is possible to derive mathematical relationships for the asymptotes; we will not present this material in this presentation.)

Many PFs are essentially special or limiting cases of CES functions, the main characteristics of which are given in Table 4.1.

Production function and its characteristics

The essence of the production function

The technological relationship between the amount of resources expended by a firm per unit of time and the maximum possible volume of output is called the production function.

In its most general form, the production function can be written as

Q = f(X1,X2,...Xn),

where Q is the volume of output per unit of time,

X1,X2,...Xn - the amount of resources used per unit of time.

The production function characterizes the technical relationship between resources and output and describes the entire set of technologically efficient production methods. Each production method (technology) can be described by its production function. And accordingly, a change in production technology entails a change in the function itself.

It is important to note that production that does not provide the maximum possible volume of output for a given amount of resources is considered inefficient and, according to one of the initial principles of microeconomics (the principle of rationality), is not used by a rational entrepreneur.

Like any other function, a production function can be written as a table, equation, or graph.

In microeconomics, a large number of very diverse production functions are used, but most often - two-factor functions of the form

which are easier to analyze due to the possibility of their graphical representation.

Among two-factor functions, the most famous is the function I Cobb-Douglas, having the form:

,

Where A, are positive constants;

X, Y- the amount of resources used (usually labor and capital are considered).

Knowing its production function, a firm can estimate how its output will change if it increases or decreases the amount of one input while leaving all other inputs constant, or if it increases the amount of all inputs used equally or unequally.

Short run production function

The activity of a firm in the short run can be characterized using a short-run production function, which assumes that the firm has partly constant and partly variable resources.

Where TO- amount of permanent resource;

L- amount of variable resource.

The short-run production function shows the maximum amount of output that a firm can produce by changing the quantity and combination of variable inputs, given the amount of fixed inputs.

To simplify our analysis, let us assume that the firm uses only two resources: a variable resource - labor ( L) and a constant resource - capital ( TO).

Figure 5.1 – Graphic representation of total, average and marginal products

Graphical representation of the production function

Let us present our results graphically. As can be seen from Fig. 5.1, the production function in its development passes three stages.

On first stage(for L from 0 to L3) there is an increase in the output of the variable resource (i.e., the average product APL grows and reaches its maximum APmax), the marginal product of labor MPL also increases and reaches its maximum value MPmax. Then the marginal product stops growing, and, reaching the point of its maximum (sometimes called the point of decreasing marginal product), it begins to decrease. At the same time, the average product APL continues to grow to its maximum value (in our example, APL = max at L3).

On second stage(from L3 to L4) there is a decrease in the return of the variable resource (i.e., the average product APL decreases), the marginal product MPL also continues to decrease and reaches zero (MP = 0 at L4). In this case, the volume of the total product TP becomes maximum (TPmax) possible and its further increase due to the increase in only variable resources is no longer feasible.

On third stage(from L4 onwards) the marginal product acquires a negative value (MP< 0), а совокупный продукт ТР начинает сокращаться.

To achieve the most effective results and minimize costs, the company should use a variable resource in the amount corresponding to stage II. At stage I, additional use of a variable resource leads to a reduction in average costs. At stage III, the total volume of output and average costs are reduced (i.e., profitability falls).

The reason for this behavior of the production function lies in principle (law) of diminishing marginal returns:

starting from a certain point in time, additional use of a variable resource with a constant amount of a constant resource leads to a reduction in marginal returns, or marginal product.

This law is universal in nature and is characteristic of almost all economic processes. (The Russian proverb “Seven nannies have a child without an eye” perfectly illustrates this principle).

d(APL)/dL = = 0.

Isoquant and isoquant map. Properties of isoquants

Depending on the state of market demand, a company can choose one of several production options. To accurately determine the optimal output volume, we use a graphical method of analyzing the production function through isoquants and isocosts.

Construction of an isoquant

For simplicity of analysis, as before, we will assume that:

· the production function under study depends on two factors: labor and capital,

· is a special case of the Cobb-Douglas function and has the form: Q = KL;

Factors of production will be interchangeable within certain limits;

· production technology does not change during the entire period under review.

Let us present this function for the values ​​in table form K And L from 1 to 4.

Table 6.1 – Production function

As can be seen from table. 6.1, there are several combinations of labor and capital that provide a given output volume within certain limits. For example, Q = 4 can be obtained using the following combinations of labor and capital: (1,4), (4,1) and (2,2). Similarly, Q = 6 can be obtained using combinations (2,3) and (3,2), etc.

If we plot the number of units of labor along the horizontal axis, the number of units of capital along the vertical axis, then designate the points at which the firm produces the same volume, we will get the curve shown in Fig. 6.1 and called isoquant(IQ).

Each isoquant point corresponds to a combination of resources at which the firm produces a given volume of output.

Figure 6.1 – Isoquant map

The set of isoquants characterizing a given production function is called isoquant map.

Properties of isoquants

The properties of standard isoquants are similar to those of indifference curves.

1) An isoquant, like an indifference curve, is a continuous function, and not a set of discrete points.

2) For any given volume of output, its own isoquant can be drawn, reflecting various combinations of economic resources that provide the manufacturer with the same volume of production.

3) Isoquants describing a given production function never intersect.

The intersection of isoquants would contradict the production efficiency condition. To prove this, suppose that two isoquants for different volumes have one common point A. Let's mark two more arbitrary points on the graph IN And WITH, as shown in Fig. 6.2.

Figure 6.2 – Isoquants do not intersect

Combination of resources IN is more preferable for the company than the combination WITH, since it contains a larger amount of both resources, and therefore, in accordance with a given production function, provides a larger volume of output. However, combinations A And IN belong to the same isoquant, and therefore provide the same volume of production. Combinations A And WITH also belong to the same isoquant and also provide the same volume. In accordance with the principle of transitivity, if A = B and A = C, then B = C, and this contradicts the original position.

4) Isoquants do not have increasing areas.

If an area of ​​increase existed, then when moving along it, the quantity of both the first (K) and second (L) resource would increase, i.e., the volume of maximum output would increase, and it (volume) should be constant throughout the isoquant .

The decreasing nature of the isoquant reflects the possibility of substitution within certain limits of the resources used, so that the total volume of output remains unchanged.

Limit rate of technological substitution(Marginal Rate of Technical Substitution, or MRTS) of one resource for another (for example, labor for capital) shows the degree of substitution of labor with capital, at which the volume of output remains unchanged.

An algebraic expression showing the degree to which a producer is willing to reduce the amount of capital in exchange for an increase in labor sufficient to maintain the same output is given by

Due to the negative slope of the indifference curve, this ratio will always be a negative value. Sometimes, for convenience, a minus is introduced in front of the right side, but in most cases the absolute value of the coefficient matters.

Figure 6.3 – Limit rate of technological substitution

As can be seen in Fig. 6.3, when moving from a point A exactly IN production volume remains unchanged. This means that the reduction in output as a result of a decrease in capital costs (K = K2 - K1) is compensated by an increase in output due to the use of additional labor (L = L2 - L1).

The reduction in output resulting from a decrease in capital expenditure is equal to K times the marginal product of capital, or

The increase in output due to the use of additional quantity of labor is in turn equal to the product of L times the marginal product of labor, or

Thus, we can write that

K*MPK = L*MPL

Let's write this expression differently:

K/L = MPL/MRK

The production function, which connects the amount of capital, labor and output, also allows one to calculate the marginal rate of technological substitution through the derivative of this function:

This means that graphically at any point of the isoquant the limiting degree of technological substitution is equal to the tangent of the angle of inclination of the tangent to the isoquant at this point.

It is obvious that the degree of labor substitution with capital does not remain constant when moving along the isoquant (Fig. 6.4). As you move down the curve, the absolute value of the MRTS of labor over capital decreases, as more and more labor must be used to compensate for the decrease in capital input.

Subsequently, MRTS reaches its limit (MRTS = 0), and the isoquant takes on a horizontal form. It is obvious that a further reduction in capital costs will only lead to a reduction in output volumes. Amount of capital at a point E- the minimum allowable amount of labor for a given volume of production (in the same way, the minimum allowable amount of labor for the production of a given volume takes place at the point A).

Figure 6.4 – Decrease in the marginal rate of technological substitution

The decrease in MRTS of one resource by another is typical for most production processes and is typical for all isoquants of the standard type.

Special cases of production function (isoquants of non-standard form)

Isoquants (like indifference curves) can have different configurations.

Perfect interchangeability of resources

The linear isoquant (Fig. 6.5a) assumes perfect substitutability of production resources, so that a given output can be obtained using either only labor, or only capital, or using various combinations of both resources at a constant rate of their replacement, i.e. MRTS is constant at all isoquant points.

An example is production that allows both full automation and manual production of a product.

Fixed resource usage structure

If the technological process excludes the substitution of one factor for another and requires the use of both resources in strictly fixed proportions, the production function (isoquant map) has the form of the Latin letter L, as in Fig. 6.5b. That is, there is a strict complementarity of resources. Only one method of producing a given product is known: labor and capital are combined in the only possible ratio, the marginal rate of substitution is zero.

This isoquant is sometimes called a Leontief-type isoquant, named after the American economist of Russian origin who based this type of isoquant on the input-output method he developed, which earned him the Nobel Prize in Economics.

An example of this would be the work of a digger (one shovel and one man) or the maintenance of a tower crane (one crane operator and one crane). It is impossible to increase the amount of one of the factors without a corresponding change in the amount of the other factor, therefore only angular combinations of resources will be technically effective (optimal).

Availability of several options for using resources

In Fig. Figure 6.5c shows a broken isoquant, which assumes the presence of only a few production methods (P). In this case, the marginal rate of technical substitution decreases when moving along such an isoquant from top to bottom to the right.

An isoquant of a similar configuration is used in linear programming - a method of economic analysis developed by two other Nobel laureates - T. Koopmans () and ().

Continuous but not perfect substitutability of resources

Finally, in Fig. Figure 6.5d presents an isoquant, which assumes the possibility of continuous, but not perfect substitutability of resources within certain boundaries, beyond which the replacement of one factor by another is technically impossible (or ineffective).

Figure 6.5 – Possible configurations of isoquants

Many specialists, especially engineers, entrepreneurs, and in general those whom we usually call production workers, consider the broken isoquant to be the most realistic representation of the production capabilities of most modern industries. However, traditional economic theory usually operates with smooth isoquants like the one shown in Fig. 6.5d, since their analysis does not require the use of complex mathematical methods. In addition, isoquants of this type can be considered as a kind of approximate approximation of a broken isoquant. By increasing the number of production methods and, therefore, the number of break points, we can (in the limit) represent a broken isoquant as a smooth curve.